CLASE Nº 4
FECHA: 4 DE ENERO DEL 2017
MEDIA Y VARIANZA PARA VARIABLES ALEATORIAS CONTINUAS
V(x) = E(x^2) - (E(x))^2
La media y la varianza de la v.a.c cumplen con las mismas propiedades que las v.a.d
Ejemplo:
DISTRIBUCIÓN DE PROBABILIDAD DISCRETAS
1. DISTRIBUCIÓN UNIFORME.
Una variable aleatoria tiene distribución discreta uniforme si cada uno de los resultados de su espacio muestral tiene puede obtenerse con igual probabilidad.
Ejemplo
x
|
f(x)
|
1
|
1/6
|
2
|
1/6
|
3
|
1/6
|
4
|
1/6
|
5
|
1/6
|
6
|
1/6
|
La E(x)= 21/6
La V(x)=35/12
P(x ≥ 4) = 1/2
2. DISTRIBUCIÓN DE BERMOULLI
Es un experimento en que existen dos únicos resultados. El un resultado se denomina "EXITO" con probabilidad 'p' y el otro resultado se denomina "FRACASO" con probabilidad 'q'
x ~ Be(p)
E(x) =p
V(x)=pq
Ejemplo.
Suponer que la probabilidad de éxito de un experimento es 0.2 y se realizan cinco ensayos independientes. Calcule la probabilidad que el primero y el último ensayo sean éxitos, y los tres ensayos intermedios sean fracasos.
Sean 1: El ensayo es éxito (con probabilidad 0.2)
0: El ensayo es fracaso (con probabilidad 0.8)
Entonces
P(X=1,X=0,X=0,X=0,X=1) = f(1)f(0)f(0)f(0)f(1) = (0.2)(0.8)(0.8)(0.8)(0.2) = 0.0205 = 2.05%
3. DISTRIBUCIÓN BINOMIAL
Esta distribución es muy importante y de uso frecuente. Corresponde a experimentos con características similares a un experimento de Bernoulli, pero ahora es de interés la variable aleatoria relacionada con la cantidad de “éxitos” que se obtienen en el experimento.
Características de un Experimento Binomial
a) La cantidad de ensayos n, que se realizan es finita.
b) Cada ensayo tiene únicamente dos resultados posibles: “éxito” o “fracaso”
c) Todos los ensayos realizados son independientes
d) La probabilidad p, de obtener “éxito” en cada ensayo permanece constante.
Referencia: Luis Rodriguez. (2007). Probabilidad y estadística básica para ingenieros. Quito: ESPOL
CLASE Nº 5
FECHA: 6 DE ENERO DEL 2017
En esta clase se realizaron ejercicios de distribución binomial
1. Una fábrica tiene una norma de control de calidad consistente en elegir al azar diariamente 20 artículos producidos y determinar el número de unidades defectuosas. Si hay dos o más artículos defectuosos la fabricación se detiene para inspección de los equipos. Se conoce por experiencia que la probabilidad de que un artículo producido sea defectuoso es 5%.
Encuentre la probabilidad de que en cualquier día la producción se detenga al aplicar esta norma de control de calidad.
X ̴ Bi(20,0.05)
X: V. a. discreta cantidad de artículos defectuosos.
n = 20
p = 0.05
x = 0, 1, ..., 20

Referencia: Luis Rodriguez. (2007). Probabilidad y estadística básica para ingenieros. Quito: ESPOL
CLASE Nº 6
FECHA: 11 DE ENERO DEL 2017
4. DISTRIBUCIÓN DE POISSON
La distribución de Poisson es un modelo que puede usarse para calcular la probabilidad correspondiente al número de “éxitos” que se obtendrían en una región o en intervalo de tiempo especificados, si se conoce el número promedio de “éxitos” que ocurren.
Este modelo requiere que se cumplan las siguientes suposiciones:
a) El número de “éxitos” que ocurren en la región o intervalo es independiente de lo que ocurre en otra región o intervalo.
b) La probabilidad de que un resultado ocurra en una región o intervalo muy pequeño, es igual para todos los intervalos o regiones de igual tamaño y es proporcional al tamaño de la región o intervalo.
c) La probabilidad de que más de un resultado ocurra en una región o intervalo muy pequeño no es significativa.
Algunas situaciones que se pueden analizar con este modelo:
- Número de defectos por unidad de área en piezas similares de un material.
- Número de personas que llegan a una estación en un intervalo de tiempo especificado.
- Número de errores de transmisión de datos en un intervalo de tiempo dado.
- Número de llamadas telefónicas que entran a una central por minuto.
- Número de accidentes automovilísticos producidos en una intersección, en una semana.
Referencia: Luis Rodriguez. (2007). Probabilidad y estadística básica para ingenieros. Quito: ESPOL
CLASE Nº 7
x ~ H(x,N,k,n)
E(x) =n(k/N)
V(x)=n(k/N)(1-k/N)((N-n/N-1))
Aproximación de la distribución hipergeométrica a la distribución binomial
Si se cumple que n<5%N, entonces x~H(x,N,k,n) -------> x~Bi(n,p) donde p=k/N
6. DISTRIBUCIÓN BINOMIAL NEGATIVA
Este modelo de probabilidad tienen características similares al modelo binomial: los ensayos son independientes, cada ensayo tiene únicamente dos resultados posibles, y la probabilidad que cada ensayo tenga un resultado favorable es constante. Pero, en este modelo la variable aleatoria es diferente:
"En la Distribución Binomial Negativa, la variable de interés es la cantidad de ensayos que se realizan hasta obtener un número requerido de éxitos, k"
x ~ BN(k,p)
E(x) =k/p
V(x)=k/p(1/p-1)
EJEMPLO
7. DISTRIBUCIÓN GEOMÉTRICA
Es un caso especial de la distribución binomial negativa, cuando k=1. Es decir interesa conocer la probabilidad respecto a la cantidad de ensayos que se realizan hasta obtener el primer “éxito”
x ~ G(p)
E(x) =1/p
V(x)=1/p(1/p-1)
Referencia: Luis Rodriguez. (2007). Probabilidad y estadística básica para ingenieros. Quito: ESPOL
CLASE Nº 8
FECHA: 18 DE ENERO DEL 2017
DISTRIBUCIONES DE PROBABILIDAD CONTINUAS
1. DISTRIBUCIÓN UNIFORME (Probabilidad en un intervalo)
Este modelo corresponde a una v.a.c cuyos valores tienen igual valor de probabilidad en un intervalo especifico para una variable.
MEDIA VARIANZA DE LA DISTRIBUCIÓN UNIFORME CONTINUA
Para mayor información:
CASO ESPECIAL
Para generalizar y facilitar el cálculo de probabilidad con la distribución Normal, es conveniente definir la Distribución Normal Estándar que se obtiene haciendo μ = 0, y σ2 = 1 en la función de densidad de la Distribución Normal
ESTANDARIZACIÓN DE LA DISTRIBUCIÓN NORMAL
EJEMPLO
La duración de un evento tiene la distribución normal con media 10. varianza 4. Encuentre la probabilidad de que el evento dure:
a) Menos de 9 horas
b)Entre 11 y 12
Referencia: Luis Rodriguez. (2007). Probabilidad y estadística básica para ingenieros. Quito: ESPOL.
CLASE Nº 9
APROXIMACIÓN DE LA DISTRIBUCIÓN BINOMIAL CON LA DISTRIBUCIÓN NORMAL ESTÁNDAR
Sea X una variable aleatoria discreta con distribución Binomial con media μ =np, y varianza
σ2 = np(1-p)
Entonces, el límite de la distribución de la variable aleatoria

Es la distribución Normal Estándar: N(0,1)
Referencia: Luis Rodriguez. (2007). Probabilidad y estadística básica para ingenieros. Quito: ESPOL.
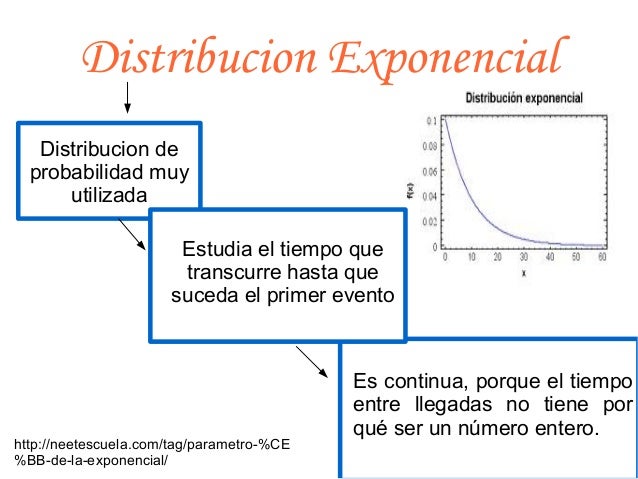
CLASE Nº 11
RELACIÓN ENTRE LAS DISTRIBUCIONES EXPONENCIALES Y POISSON
Sea x la variable que cuenta el número de eventos que ocurren en el tiempo (0,t) con MEDIA; λt entonces:

Sea T el tiempo que trascurre hasta que sucede el primer cuento de Poisson, el rango de T es ( 0, + infinito( y su función de distribución.
Donde 

El evento (T >t ) indica que el primer evento Poisson ocurre después de t, es decir:
(T>t) = (x=0)
También se puede decir

Para mayor información y ejercicios ir aqui






























No hay comentarios:
Publicar un comentario