CLASE Nº1
Fecha: 12 de Octubre del 2016
INDICACIONES GENERALES
VALORES
Se valorará ante todo el respeto y el compañerismo en la relación docente-estudiante y entre estudiantes
Se valorará ante todo el respeto y el compañerismo en la relación docente-estudiante y entre estudiantes
ASISTENCIA y PUNTUALIDAD
Se deberá justificar la inasistencia
Los atrasos (máximo 10 min)
ACTIVIDADES Y TAREAS
- Las actividades y tareas
estarán detalladas en esta sección
- Para la realización de las
tareas de forma digital se deben tener en cuenta las siguientes
indicaciones:
Crear una cuenta de GMAIL
Iniciar sesión en GMAIL
Ir a GOOGLE DRIVE
Crear Carpeta TAREAS-Nombre-Apellido
Compartir la carpeta con el siguiente correo electrónico:
mantillameh@gmail.com
- Para
la realización de las tareas de forma física se deben tener en cuenta
las siguientes indicaciones:
Papel boon tamaño A4
Margen en todas las hojas usadas
Encabezado en la primera hoja que debe contener:
Escuela Politécnica Nacional
Carrera
Materia
Nombre
Fecha
Tema
- Presentar en la fecha
señalada, se valorará la responsabilidad y cumplimiento
- Una vez registrada la tarea
y devuelta con la firma, escanear y subir al Portafolio Estudiantil en la
sección EVIDENCIAS.
- El Portafolio
Estudiantil personal es un blog que debe contener:
1. CONTEXTO
¿Quienes somos?
¿Donde estamos?
¿Qué?
¿Para qué?
Nombre completo del estudiante y fotografía
2. Un breve resumen de temas revisados en clases para cada mes
3.EVIDENCIAS: Los enlaces a los documentos creados en Google-Drive con las imágenes de las tareas ya registradas.
3.EVIDENCIAS: Los enlaces a los documentos creados en Google-Drive con las imágenes de las tareas ya registradas.
EVALUACIONES
Item
|
Porcentaje
|
Actividades, tareas
y Portafolio
Estudiantil
|
20
%
|
Evaluación
1
|
20%
|
Evaluación
2
|
20%
|
Examen
Parcial
|
40%
|
REFERENCIA: https://sites.google.com/site/probabilidadyestadistica2016b/anuncios-1
CLASE Nº2
Fecha: 12 de Octubre del 2016
CLASE Nº2
Fecha: 12 de Octubre del 2016
Introducción
La Estadística estudia usos y análisis provenientes de una muestra representativa de datos, busca explicar las correlaciones y depende de un fenómeno físico o natural, de ocurrencias en forma aleatoria o condicional.
La Estadística para su mejor estudio se ha dividido en: Estadística Descriptiva y la Inferencial.
Estadística Descriptiva: Consiste en la presentación de datos en forma de tablas y gráficas. Esta comprende cualquier actividad relacionada con los datos y está diseñada para resumir o describir los mismos sin factores pertinentes adicionales; esto es, sin intentar inferir nada que vaya más allá de los datos, como tales.
Estadística Inferencial: consiste en llegar a obtener conclusiones o generalizaciones que sobrepasan los límites de conocimiento aportados por un conjunto de datos. Busca obtener información sobre la población basándose en el estudio de los datos de una muestra tomada.
A.- DEFINICIONES DE:
Unidad muestral: Es cada una de los miembros individuales de una población.
Muestra: Constituye un subconjunto de una población, que contiene elementos o resultados que realmente se observan.
Población: Conjunto de individuos en un lugar determinado.
B.- TIPOS DE DATOS
Son numéricos y categóricos.
Numérico o Cuantitativo
Discretos: Los cuales se puede contar (conteos) como por ejemplo: Numero de hijos, número de facturas, número de vehículos.
Continuos: No se puede contar exactamente puede existir decimales, como por ejemplo: peso (Kg, lb), estatura (m, cm, pies), temperatura ( °F, °K, °C ), ventas ( dólares, euros).
Categórico o Cualitativo
Expresa características o cualidades.
C.-Escalas de medición
Nominal: Usa nombres para establecer categorías, puede usar números pero estos son de carácter simbólico como por ejemplo; se puede establecer la categoría sexo con dos niveles, masculino (M) y femenino (F).
Ordinal: Se establecen categorías con dos o mas niveles que implican un orden inherente entre si. La escala de medición ordinal es cuantitativa porque permite ordenar a los eventos en función de la mayor o menor posesión de un atributo o característica. Ejemplo: mucho poco nada.
De intervalo: La medición de intervalo posee las características de la medición nominal y ordinal. Establece la distancia entre una medida y otra. La escala de intervalo se aplica a variables continuas pero carece de un punto cero absoluto. Ejemplo: Una persona que en un examen de matemáticas que obtiene una puntuación de cero no significa que carezca de conocimientos, el punto cero es arbitrario por que sigue existiendo la característica medida.
De razón: Una escala de medición de razón incluye las características de los tres anteriores niveles de medición anteriores (nominal, ordinal e intervalo). Determina la distancia exacta entre los intervalos de una categoría. Adicionalmente tiene un punto cero absoluto, es decir, en el punto cero no existe la característica o atributo que se mide. Las variables de ingreso, edad, número de hijos, etc. son ejemplos de este tipo de escala. El nivel de medición de razón se aplica tanto a variables continuas como discretas.
La Estadística estudia usos y análisis provenientes de una muestra representativa de datos, busca explicar las correlaciones y depende de un fenómeno físico o natural, de ocurrencias en forma aleatoria o condicional.
La Estadística para su mejor estudio se ha dividido en: Estadística Descriptiva y la Inferencial.
Estadística Descriptiva: Consiste en la presentación de datos en forma de tablas y gráficas. Esta comprende cualquier actividad relacionada con los datos y está diseñada para resumir o describir los mismos sin factores pertinentes adicionales; esto es, sin intentar inferir nada que vaya más allá de los datos, como tales.
Estadística Inferencial: consiste en llegar a obtener conclusiones o generalizaciones que sobrepasan los límites de conocimiento aportados por un conjunto de datos. Busca obtener información sobre la población basándose en el estudio de los datos de una muestra tomada.
A.- DEFINICIONES DE:
Unidad muestral: Es cada una de los miembros individuales de una población.
Muestra: Constituye un subconjunto de una población, que contiene elementos o resultados que realmente se observan.
Población: Conjunto de individuos en un lugar determinado.
B.- TIPOS DE DATOS
Son numéricos y categóricos.
Numérico o Cuantitativo
Discretos: Los cuales se puede contar (conteos) como por ejemplo: Numero de hijos, número de facturas, número de vehículos.
Continuos: No se puede contar exactamente puede existir decimales, como por ejemplo: peso (Kg, lb), estatura (m, cm, pies), temperatura ( °F, °K, °C ), ventas ( dólares, euros).
Categórico o Cualitativo
Expresa características o cualidades.
C.-Escalas de medición
Nominal: Usa nombres para establecer categorías, puede usar números pero estos son de carácter simbólico como por ejemplo; se puede establecer la categoría sexo con dos niveles, masculino (M) y femenino (F).
Ordinal: Se establecen categorías con dos o mas niveles que implican un orden inherente entre si. La escala de medición ordinal es cuantitativa porque permite ordenar a los eventos en función de la mayor o menor posesión de un atributo o característica. Ejemplo: mucho poco nada.
De intervalo: La medición de intervalo posee las características de la medición nominal y ordinal. Establece la distancia entre una medida y otra. La escala de intervalo se aplica a variables continuas pero carece de un punto cero absoluto. Ejemplo: Una persona que en un examen de matemáticas que obtiene una puntuación de cero no significa que carezca de conocimientos, el punto cero es arbitrario por que sigue existiendo la característica medida.
De razón: Una escala de medición de razón incluye las características de los tres anteriores niveles de medición anteriores (nominal, ordinal e intervalo). Determina la distancia exacta entre los intervalos de una categoría. Adicionalmente tiene un punto cero absoluto, es decir, en el punto cero no existe la característica o atributo que se mide. Las variables de ingreso, edad, número de hijos, etc. son ejemplos de este tipo de escala. El nivel de medición de razón se aplica tanto a variables continuas como discretas.
CLASE Nº 3Fecha: 26 de Octubre del 2016
RESUMEN ESTADÍSTICO
- Es una serie de cantidades calculadas para caracterizar a la muestra.
- Se pretende describir las características de los individuos de la muestra.
Las principales o más comunes son:
MODA O PROMEDIO
La media muestral también se llama “media aritmética”, o, simplemente, “promedio”. Representa la suma de los números en la muestra, dividido entre la cantidad total de números que hay. La media se calcula:

DESVIACIÓN ESTÁNDAR.
Es una cantidad que mide el grado de dispersión de una muestra. La idea básica de la desviación estándar es que cuando la dispersión es grande, los valores de la muestra tenderán a alejarse de su media, pero cuando la dispersión es pequeña los valores tendrán a alejarse de su media pero cuando la dispersión es pequeña los valores tendrán a acercarse a su media.

VARIANZA
Promedio de las desviaciones al cuadrado, excepto que lo dividamos entre n-1 en lugar de n. Se de nota s elevado al cuadrado.
DATOS ATÍPICOS
Un valor atípico es una observación extrañamente grande o pequeña. Los valores atípicos pueden tener un efecto desproporcionado en los resultados estadísticos, como la media, lo que puede conducir a interpretaciones engañosas.
TODO GRÁFICO DEBE TENER:
- Título
- Numeración (Gráfico N°1)
- Título de los ejes
- Escala adecuada de los ejes
- Descripción de la gráfica
- Interpretación del gráfico
EJEMPLOS:
Una muestra aleatoria simple de cinco hombres se elige de entre una gran población de Hombres y se mide su estatura. Las cinco cifras de estatura (en pulgadas) son 65.51, 72.30, 68.31, 67.05 y 70.68. Encuentre la media muestral.
Solución
X =1/5(65.51 + 72.30 + 68.31 + 67.05 + 70.68) = 68.77 pulgadas.
REFERENCIAS
Navidi, W. Resumen Estadístico. Estadística para ingenieros y Científicos. Ed. Mc Graw Hill, S.A, México, 1era ed, 2006
CLASE Nº4
Mediana Muestral
La media recortada
De la misma manera que la mediana, la media recortada es una medida de tendencia central que se diseñó para que no esté afectada por datos atípicos. La media recortada se calcula al arreglar los valores de la muestra en orden, “recortar” un número igual a partir de cada extremo y calcular la media de los restantes. Si se “recorta” el p% de los datos de cada extremo, la media recortada resultante se denomina “media recortada un p%”.
De la misma manera que la mediana, la media recortada es una medida de tendencia central que se diseñó para que no esté afectada por datos atípicos. La media recortada se calcula al arreglar los valores de la muestra en orden, “recortar” un número igual a partir de cada extremo y calcular la media de los restantes. Si se “recorta” el p% de los datos de cada extremo, la media recortada resultante se denomina “media recortada un p%”.
La moda y el rango
La moda y el rango son resúmenes estadísticos de uso limitado, pero que en ocasiones se
aprecian visualmente.
La moda muestral es el valor que tiene más frecuencia en una muestra Si algunos valores tienen una frecuencia igual, cada uno representa una moda.
El rango es la diferencia entre los valores más grandes y más pequeños en una muestra.
PERCENTILES (Pk)
Son cada uno de los 99 valores que dividen el rango en 100 partes iguales.
i) 1% Pk
ii) 25% Cuartiles
iii) 20% Quintiles
Cálculo de los percentiles
i) Para datos individuales
Pk: Xt+Xt+1/ 2 Si r= 0
Pk: Xt+1 Si r es mayor que 0
t: Parte fraccionaria de la expresión nk/100
r: Parte fraccionaria de la expresión
k: Orden del percentil
Diagramas de caja
Un diagrama de caja constituye una gráfica que incluye la mediana, el primero y el tercer
cuartil y cualquier dato atípico que se presente en una muestra.
COEFICIENTE DE VARIANZA
Cv= S/x
Si Cv<1 son datos homogeneos
Si Cv>1 son datos heterogeneos
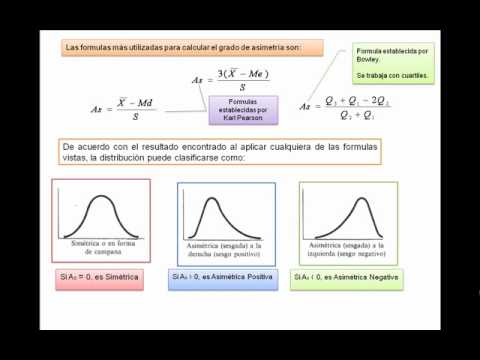
COEFICIENTE DE ASIMETRIA
Mide el grado de simetría que presenta un conjunto de datos.
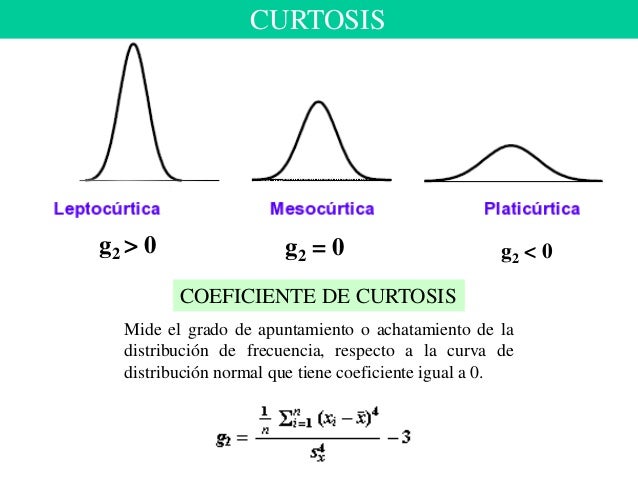
COEFICIENTE DE APUNTAMIENTO O CORTOSIS
Mide el grado de concentración de la distribución de datos alrededor de la media.
La moda y el rango son resúmenes estadísticos de uso limitado, pero que en ocasiones se
aprecian visualmente.
La moda muestral es el valor que tiene más frecuencia en una muestra Si algunos valores tienen una frecuencia igual, cada uno representa una moda.
El rango es la diferencia entre los valores más grandes y más pequeños en una muestra.
PERCENTILES (Pk)
Son cada uno de los 99 valores que dividen el rango en 100 partes iguales.
i) 1% Pk
ii) 25% Cuartiles
iii) 20% Quintiles
Cálculo de los percentiles
i) Para datos individuales
Pk: Xt+Xt+1/ 2 Si r= 0
Pk: Xt+1 Si r es mayor que 0
t: Parte fraccionaria de la expresión nk/100
r: Parte fraccionaria de la expresión
k: Orden del percentil
Diagramas de caja
Un diagrama de caja constituye una gráfica que incluye la mediana, el primero y el tercer
cuartil y cualquier dato atípico que se presente en una muestra.
CARACTERÍSTICAS DE LOS DATOS
- Localización: Media, Mediana, Moda, Percentiles
- Dispersión: Rango, Variacion, Desviación, Rango Intercuartil (Q3-Q3), Coeficiente de variación
- Simetría: Coeficiente de simetría, Coeficiente de apuntamiento.
COEFICIENTE DE VARIANZA
Cv= S/x
Si Cv<1 son datos homogeneos
Si Cv>1 son datos heterogeneos
COEFICIENTE DE ASIMETRIA
Mide el grado de simetría que presenta un conjunto de datos.
COEFICIENTE DE APUNTAMIENTO O CORTOSIS
Mide el grado de concentración de la distribución de datos alrededor de la media.
NOTA: Todas estas medidas son para datos cuantitativos. Para datos cualitativos o categoricos solo se calcula la moda y proporciones.



No hay comentarios:
Publicar un comentario