NOVIEMBRE

CLASE Nº 5

FECHA: 9 DE NOVIEMBRE DEL 2016

EJERCICIO

En una empresa financiera, los empleados disponen de computadoras portátiles de distintas marcas, un resumen del numero de maquinas, de acuerdo a su respectiva marca se observa en el siguiente cuadro

x= marcas de computadores portátiles.

Mo= Marca Toshiba

DIAGRAMA DE BARRAS

Descripción: el gráfico de barras representa la frecuencia relativa de las marcas de computadores portátiles de una empresa financiera.

Interpretación: En el gráfico la marca toshiba es la que tiene mayor frecuencia y con menor frecuencia es la que no se sabe la marca

DIAGRAMA CIRCULAR O SECTORES

DATOS AGRUPADOS EN INTERVALOS O CLASES

DISTRIBUCIÓN DE FRECUENCIAS

1) Decidir el # de clase o intervalos.

Fórmula empirica

k= 1 + 3,3log(n)     ; k= #de clases o intervalos

                               ; n = # de observaciones

2) Calcular la longitud de Clase (A)

A= (Xmáx - Xmín)/k

3) Construir las clases o intervalos

4) Calcular las columnas de la tabla de frecuencias.

Ejercicio

La inversión anual de miles de $ de una muestra de 40 pequeñas empresas fueron

36 19 29 37 33 22 29 31 21 35

20  4  25 34 24 27 27 24 26 31

27 17 31 10 28 15 41 30 18 39

46 26 12 23 18 35 25 28 23 28

a) Elabore una distribución de frecuencias

b) Realice un diagrama de tallo y hojas

c) Realice un histograma

d) Determine el % de empresas con una inversión entre 14 mil y 20 mil dólares

x= inversión en miles de dólares de pequeñas empresas (cuantitativa)

n=40   ; k=6

A= (46-4)/6=7

a)

b) 

c) 

Descripción: El presente gráfico representa la frecuencia absoluta de las inversiones de pequeñas empresas.

Interpretación: En el gráfico se ve que no existe una distribución simetrica, mas bien es asimétrica, ademas se ve que existen 16 empresas entre 25 y 32 mil dolares de inversión.

d) El 11,4%  representa el porcentaje de empresas que invierten entre 14 y 20 mil dolares 

CLASE Nº 6

FECHA: 11 DE NOVIEMBRE DEL 2016

En esta clase se realizaron ejercicios

Ejemplos 






CLASE Nº 7

FECHA: 16 DE NOVIEMBRE DEL 2016

En esta clase se realizó la actividad de el Corazón.  Disponible en Taller 1


.
CLASE Nº 8

FECHA: 18 DE NOVIEMBRE DEL 2016

MUESTRAS BIVARIADAS

Dos variables para una misma muestra.


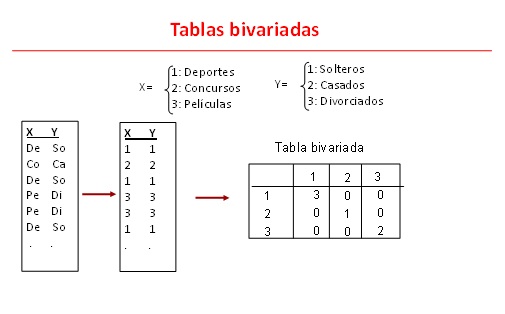
i) Identificar variables, "x" y "y"

ii) Diagrama de dispersión.



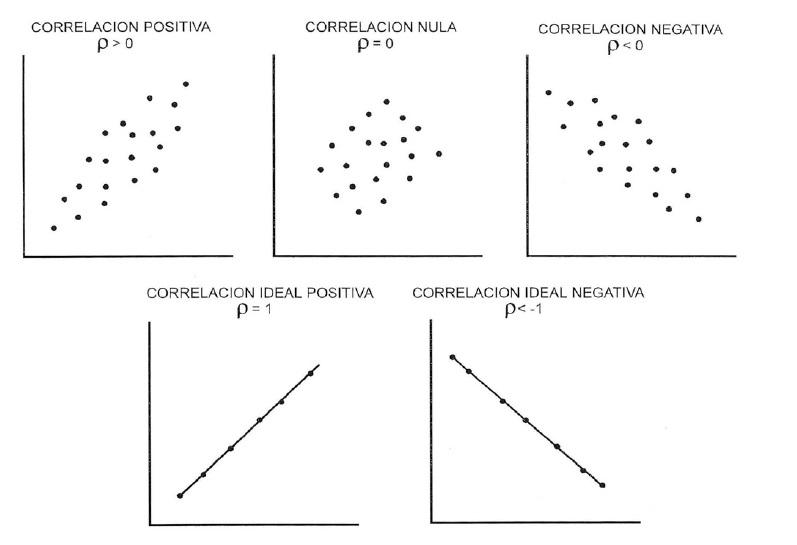
CORRELACIÓN: Relación que presentan las variables relacionadas.

COVARIANZA MUESTRAL

Sean
x,y: variables muestrales
n: tamaño de la muestra
x, y : medias muestrales
Sx: raíz de (Sx°2)
Sy: raíz de (Sx°2) desviaciones estándar x e y
Sxy: covarianza muestral




La covarianza es una medida de la correlación entre las variables.
Si Sxy es mayor que 0 entonces la tendencia es lineal positiva
Si Sxy es menor que 0 entonces la tendencia es lineal negativa

COEFICIENTE DE CORRELACIÓN (r)



                     r=Sxy/SxSy
-1 menor o igual que r menor que igual que 1

MATRIZ DE VARIANZA-COVARIANZA

MATRIZ DE CORRELACIÓN



EJEMPLO ILUSTRATIVO



CLASE Nº 9

FECHA: 19 DE NOVIEMBRE DEL 2016

En esta clase rendimos la primera prueba bimestral. Evaluación 1

Corrección de Evaluación 1.


CLASE Nº 10

FECHA: 23 DE NOVIEMBRE DEL 2016

PROBABILIDAD

Medida cuantitativa de que tan probable es que ocurra un evento.

Ideas Básicas.

Experimento: es un proceso con un resultado que no se puede predecir certeramente con anterioridad.

Espacio Muestral: conjunto de todos los posibles resultados de un experimento.

Evento: Subconjunto del espacio muestral.

Eventos mutuamente excluyentes:

- No tienen resultados en común.

- Una colección de eventos es mutuamente excluyente si no tienen resultados en común.

COMBINACIÓN DE EVENTOS

También pueden mostrarse en forma de diagrama de ven

Dado un experimento y cualquier evento A:

• La expresión P(A) denota la probabilidad de que ocurra el evento A.
• P(A) constituye la proporción de veces que se presenta el evento A en el tiempo, si es que el experimento se realizara una y otra vez.

AXIOMAS DE PROBABILIDAD

DIAGRAMA DEL ÁRBOL

Referencia:

Navidi, W. Resumen Estadístico. Estadística para ingenieros y Científicos. Ed. Mc Graw Hill, S.A, México, 1era ed, 2006




CLASE Nº 11

FECHA: 25 DE NOVIEMBRE DEL 2016

MÉTODOS DE CONTEO

Principio Fundamental

Si una operación se puede realizar de n maneras, y si cada una de estas n maneras se puede realizar una segunda operación de n2 maneras, entonces el número total de maneras en que se realizan las dos operaciones es n*n2...

Ejemplo:

Cierto tipo de automóvil se encuentra disponible en tres colores: rojo, azul o verde, y puede tener un motor grande o pequeño. ¿De cuántas maneras puede un comprador elegir un automóvil?


Tamaño del motor:  n1= 2
Color del automovil: n2 =3

n1 * n2= (2) (3) = 6

Número total de maneras de elegir = 6

PERMUTACIONES

- Es un ordenamiento de un conjunto de n elementos.
- El número de permutaciones de n elementos es n!

n! = n(n-1)(n-2)....2(1)

0! = 1

1!= 1

Ejemplo: 

¿ Cual es el número de permutaciones de arreglos con las letras: A, B, C?

Si A, B, C ------ n=3------ =3!

                                          =6              [ ABC, BAC, BCA, ACB, CAB, CBA ]

PERMUTACIONES DE k ELEMENTOS

El numero de permitaciones de k elementos de un total de n elementos.

                             

Ejemplo:

Un grupo de 10 personas puede elegir a su directiva: presidente, secretario, tesorero. Todos pueden ser elegidos, pero una persona no puede tener mas de un cargo. De cuantas maneras diferentes puede realizarse la elección.

k=3                          3P10 = (10!)/(10-3)!= 720

n=10

Otra forma: 

10(9)(8)= 720

Casos particulares:

- Se puede presentar que el arreglo sea circular, entonces el número de permutaciones es (n-1)!



Para mayor información revisar los siguientes ejemplos: EJEMPLOS


COMBINACIONES

Son arreglos de k elementos elegidos de un grupo de n elementos. En estos arreglos el orden no importa.

Ejemplo:

CLASE Nº 12

FECHA: 30 DE NOVIEMBRE DEL 2016

En esta clase se realizaron ejercicios relacionados con el tema anterior

Ejercicio 1

En una habitación se encuentra el siguiente grupo de personas: 5 hombres mayores de 21, 4 menores de 21, 6 mujeres mayores de 21, 3 mujeres menores de 21. Se elige una persona al azar y se definen los siguientes sucesos:

a: La persona es mayor de 21

b: La persona es menor de 21

c: La persona es hombre

d: La persona es mujer

Evaluar las siguientes probabilidades:

a)  P(BUD)

b)  P(AUC)

c)  P(A^cUB^c)

Experimento: Selección de una persona de una habitación

P(B) = 7/18   ;   P(D) = 9/18  ;  P(B∩D) = 3/18

a)  P(BUD) = P(B) + P(D) - P(B∩D) 

                   = 7/18 + 9/18 - 3/18 = 13/18

P(A) = 11/18   ;  P(C) = 9/18  ;  P(A∩C) = 5/18

b) P(AUC) = 11/18 + 9/18 - 5/18= 15/18

P(A^c) = 7/11  ;  P(B^c) = 11/18  ;  P(A^c∩ B^c) = 0

c)  P(A^cUB^c) = 7/18 +11/18 =1

Probabilidad condicionada